sphdpa() computes the angular distance and generalized position angle (see notes) from a "reference" point to a number of "field" points on the sphere. The points must be specified consistently in any spherical coordinate system.
- Parameters:
-
| [in] | nfield | The number of field points. |
| [in] | lng0,lat0 | Spherical coordinates of the reference point [deg]. |
| [in] | lng,lat | Spherical coordinates of the field points [deg]. |
| [out] | dist,pa | Angular distance and position angle [deg]. |
- Returns:
- Status return value:
Notes:
sphdpa() uses
sphs2x() to rotate coordinates so that the reference point is at the north pole of the new system with the north pole of the old system at zero longitude in the new. The Euler angles required by
sphs2x() for this rotation are
eul[0] = lng0;
eul[1] = 90.0 - lat0;
eul[2] = 0.0;
The angular distance and generalized position angle are readily obtained from the longitude and latitude of the field point in the new system.
It is evident that the coordinate system in which the two points are expressed is irrelevant to the determination of the angular separation between the points. However, this is not true of the generalized position angle.
The generalized position angle is here defined as the angle of intersection of the great circle containing the reference and field points with that containing the reference point and the pole. It has its normal meaning when the the reference and field points are specified in equatorial coordinates (right ascension and declination).
Interchanging the reference and field points changes the position angle in a non-intuitive way (because the sum of the angles of a spherical triangle normally exceeds 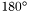 ).
).
The position angle is undefined if the reference and field points are coincident or antipodal. This may be detected by checking for a distance of 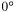 or
or 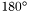 (within rounding tolerance). sphdpa() will return an arbitrary position angle in such circumstances.
(within rounding tolerance). sphdpa() will return an arbitrary position angle in such circumstances.
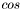 (eul[1])
(eul[1])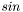 (eul[1])
(eul[1]) 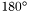 ).
).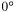 or
or  1.5.1
1.5.1